Enuncia el Teorema fundamental del cálculo
Necesito contestar esto pero no tengo idea ojala me puedan apoyar
Calcular las siguientes integrales indefinidas y verificar su resultado por derivación.
1 respuesta
·
·
¡Hola Angels!
Es verdad que yo siempre había oído hablar de un teorema fuldamental del cálculo y de la regla de Barrow. Pero en otros escritos, la Wikipedia sin ir más lejos habla de dos teoremas fundamentales. Conste que para mí el que sirve es el primero, pero te pongo los dos:
·
·
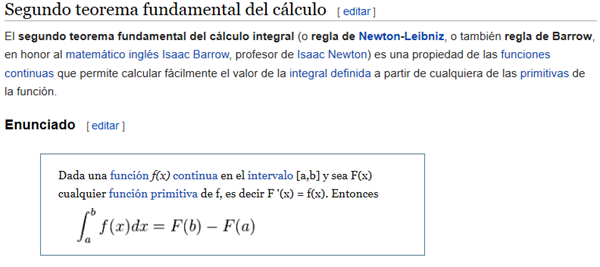
Lo que diga tu libro o apuntes es lo que debe prevalecer.
Las ventajas son sobre todo a la hora de realizar integrales, que mediantes sumas de Riemann por ejemplo serían harto difíciles o cuanto menos muy pesadas de realizar.
$$\begin{align}&\int (12x^{-3}-4senx)dx=\\&\\&12·\frac{x^{-2}}{-2}-4(-\cos x)+C)=\\&\\&-6x^{-2}+4 \cos x+C\\&\\&\\&\\&\int(-3cos x+ 4 csc x) dx=\\&\\&-3senx + ¿?+C\\&\\&\text{La integral de la cosecante es dificilísima}\\&\text{comparada con las otras. A no ser que te}\\&\text{la hayan dado como directa es muy complicada}\\&\text{de resolver.}\\&\\&\\&\\&\int \sqrt[3]{x^2}dx=\int x^{\frac 23}dx=\frac{x^{5/3}}{\frac 53}+C=\\&\\&\frac 35 \sqrt[3]{x^5}+C\end{align}$$Esa segunda integral que digo que parece tan difícil aparte está mal excrita, cox no es nnguna función trigonométrica pese a que he supuesto que era el coseno de x.
Saludos.
:
:
