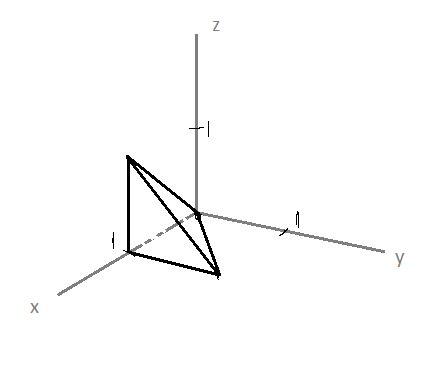Me podrían decir como hallo la ec. Del tetraedro en esta integral triple

Ya que la figura es sencilla podemos hacer un boceto para ayudarnos

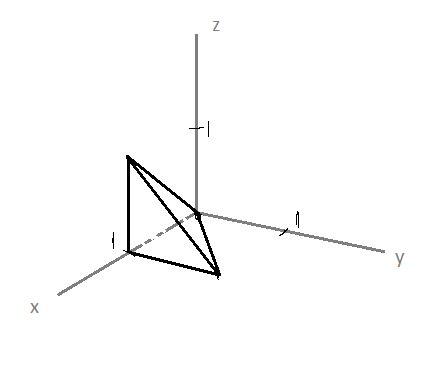
• Veamos la ecuación del segmento de extremos (0,0,0) y (1,1,0) en el plano XY

$$\begin{align}&y=x~,~para ~x\in[0,1]\end{align}$$

Pero como queremos la región por "debajo" de tal segmento entonces el conjunto que define al triángulo en el plano XY es

$$\begin{align}&R_{xy}=\{(x,y):0\leq x\leq1~,~0\leq y\leq x\}\end{align}$$

• Como las paredes laterales del tetraedro son perpendiculares al plano XY entonces nos interesará la ecuación del plano que pasa por los puntos (0,0,0) , (1,0,1) & (1,1,0)

$$\begin{align}&x-y-z=0\end{align}$$

por ende el tetraedro se define como

$$\begin{align}&S=\{(x,y,z): 0\leq x \leq 1 ~,~ 0\leq y \leq x ~,~ 0\leq z\leq x-y\}\end{align}$$